Skip to content

Report 20250901

论文：KITS

title: KITS: Inductive Spatio-Temporal Kriging with Increment Training Strategy

arxiv: https://arxiv.org/abs/2311.02565

创新点

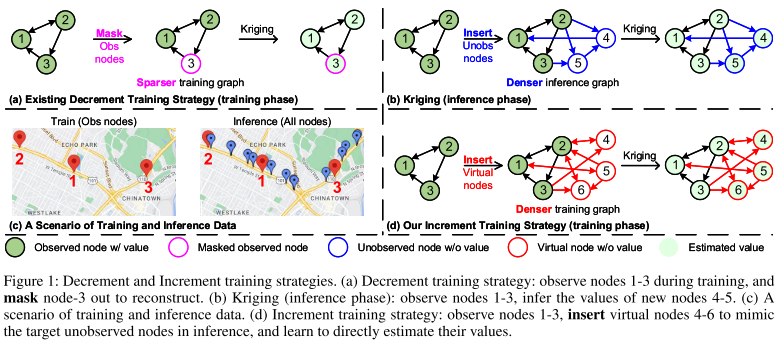
  1. 提出增量训练策略（Increment Training Strategy），解决 “图间隙” 问题：现有方法普遍采用减量训练策略（Decrement Strategy）：在训练阶段仅基于观测节点构建图，通过 “掩盖部分观测节点值并重构” 模拟推理阶段的未观测节点。但该策略存在严重的图间隙问题—— 训练图仅包含观测节点（稀疏），而推理图包含观测 + 未观测节点（密集），两者节点数量、拓扑结构差异显著（实验显示训练图平均节点度比推理图低 70% 以上），导致模型泛化能力差。

  2. 设计基于参考的特征融合模块（Reference-based Feature Fusion, RFF），解决 “特征质量差距” 问题：增量策略中，虚拟节点无真实标签，初始特征质量远低于观测节点，易导致 “观测节点过拟合、虚拟节点欠拟合”。RFF 通过 “节点对齐 + 特征融合” 弥合两者特征差距

  3. 提出节点感知循环调节（Node-aware Cycle Regulation, NCR），为虚拟节点提供监督信号：虚拟节点无真实标签，缺乏训练监督，NCR 通过 “两次克里金推理 + 伪标签构建” 为虚拟节点注入可靠监督

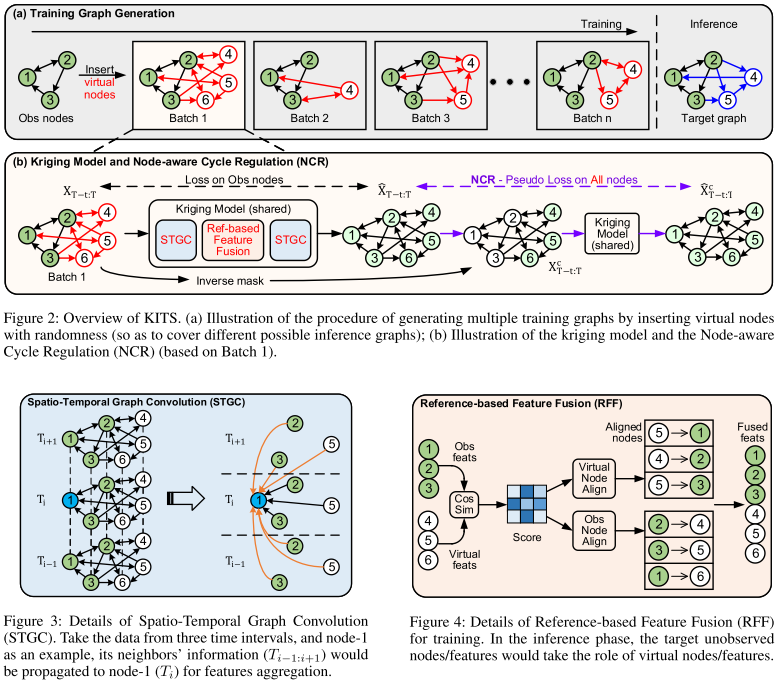
image-20250831114921460

image-20250831114921460

模块构成

  1. 增量训练图生成模块：Training Graph Generation

    1. 构成：
      1. 输入：观测节点集合N_o、预估缺失率\alpha、观测节点邻接矩阵A^o；
    2. 步骤：
      1. 虚拟节点数量计算：计算虚拟节点数量N_v=\frac{\alpha·N_o}{1-\alpha}并初始化特征为0，并加入随机噪声\varepsilon已适配不同的缺失率场景，此时虚拟节点还没有真实值
      2. 虚拟节点连边规则：为每个虚拟节点随机选择一个观测节点作为“锚点”，并以均匀分布概率p\sim Uniform[0,1]与锚点的一阶邻居连边，按“锚边+随机连边”规则构建虚拟节点与观测节点的连边，生成扩展邻接矩阵A\in \mathbb{R}^{(N_o+N_v)\times (N_o+N_v)}
      3. 生成多批次不同的训练图，提升模型对推理图的适配性
    3. 作用
      1. 缩小训练图与推理图的拓扑差距，为后续模块提供贴近推理场景的训练数据
    4. 为什么虚拟节点是这样计算：
      1. 要尽可能保持训练阶段的缺失率和推理节点相同，定义损失率为\alpha
      2. 推理图中\alpha=\frac{N_u}{N_o+N_u}，其中N_o是观测节点数，N_u是为观测节点数（要推理出的节点）
      3. 训练图中\alpha=\frac{N_v}{N_o+N_v}，其中N_o是观测节点数，N_v是为虚拟节点数
      4. 所以N_v=\frac{\alpha·N_o}{1-\alpha}
    5. 随机噪声\varepsilon：
      1. 实际场景中推理节点的真是缺失率可能与预估值\alpha存在偏差，在计算N_v时加入小范围随机噪声：N_v=\frac{(\alpha+\varepsilon)·N_o}{1-(\alpha+\varepsilon)}，其中\varepsilon\sim Uniform[-\delta,+\delta]，其中\delta为噪声幅度，实验中设置为0.05

    image-20250831114841639

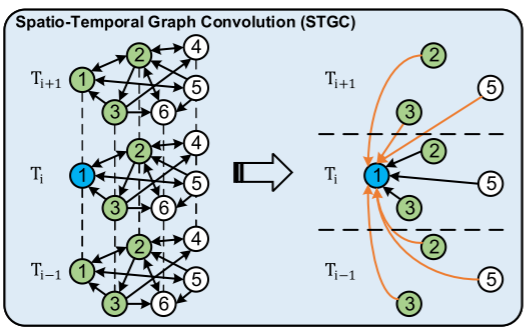
  2. 时空图卷积：STGC

    1. 步骤：
      1. 时间特征拼接：对第i个时间步的特征Z_i\in \mathbb{R}^{N\times D}，拼接前后m个时间步的特征，得到Z_{i-m:i+m}\in \mathbb{R}^{N\times (2m+1)D}，强化时间依赖
        1. D：单个节点在单个时间步的特征维度
        2. Z_i的每行对应一个节点在T_i时间步的特征向量
        3. 特征拼接方式：将T_{i-m}\sim T_{i+m}每个时间步的特征矩阵按照特征维度D拼接，得到Z_{i-m:i+m}\in \mathbb{R}^{N\times (2m+1)D}
      2. 无自环图卷积：掩盖邻接矩阵A的对角线元素（去除自环），得到A^-，避免节点从自身聚合特征（防止观测节点过拟合，虚拟节点欠拟合加剧）
      3. 特征聚合公式：Z_i^{(l+1)}=FC(GC(Z_{i-m:i+m}^{(l)},A^-))，其中GC(·)为归纳式图卷积（类似于\mathrm{GraphSAGE}），用于聚合空间特征，FC(·)为全连接层，用于调整特征维度
        1. 采用归纳式图卷积（GraphSAGE、GAT）而非转导式图卷积（如GCN），原因是：
          1. 克里金任务需要处理推理节点新增的未观测节点，转导式图卷积依赖于训练阶段固定节点集
          2. 归纳式图卷积通过“令居采样+局部聚合”，不依赖全局节点信息，可以处理动态节点集
        2. 步骤：
          1. 生成K阶空间支持矩阵（含正向、反向扩散及高阶邻居）（用于指导特征扩散）
          2. 基于支持矩阵迭代1-K阶邻居的时空特征
          3. 拼接多阶特征并通过1x1卷积映射到目标维度
      4. 公式：
        1. 时间扩展： $ Z_{i-m:i+m}^{(l)}=\mathrm{Concat}(Z_{i-m}^{(l)},Z_{i-m+1}^{(l)},...,Z_{i+m}^{(l)})\in \mathbb{R}^{N\times (2m+1)D}$
        2. 空间聚合：Z_{spatial}^{(l)}=GC(Z_{i-m:i+m}^{(l)},A^-)\in \mathbb{R}^{N\times D_{spatial}}
        3. 特征调整：Z_i^{(l+1)}=FC(Z_{spatial}^{(l)})=\sigma(W·Z_{spatial}^{(l)}+b)\in \mathbb{R}^{N\times D_{target}}，其中\sigma为\mathrm{ReLU}

    image-20250831114820753

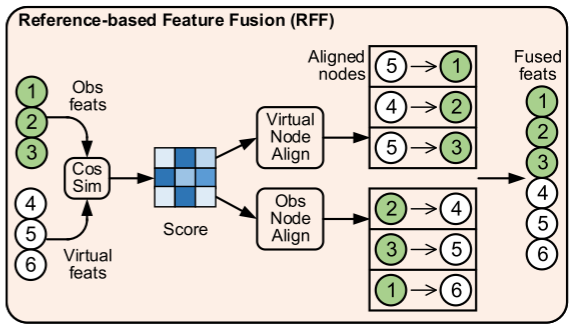
  3. 基于参考的特征融合：RFF

    1. 输入：STGC的输出的特征Z_i^{(l)}、观测节点集N^o、虚拟节点集N^v
    2. 输出：融合后的节点特征Z_i^{f_{used}}，作为最终插值估计的基础
    3. 步骤：
      1. 计算相似度矩阵：基于余弦相似度计算观测节点与虚拟节点的相似度矩阵M_s\in[0,1]^{N_o\times N_v}，量化节点间特征关联
      2. 节点双向对齐：对M_s的每行（观测节点）和每列（虚拟节点）分别取最大值，得到索引向量Ind^*，实现“每个虚拟节点匹配最相似的观测节点”“每个观测节点匹配最相似的虚拟节点”的双向对齐
      3. 特征加权融合：使用共享全连接层融合对齐节点的特征，并基于相似度向量S^*（M_s中的最大值）加权调整，公式如下：Z_i^v=FC(Z_i^v||S_i^*\odot Align(N^o,Ind^*))，其中Align(·)根据索引Ind^*提取最相似的观测节点的特征，\odot为元素积。该模块让虚拟节点借鉴观测节点的优质特征，同时避免观测节点过拟合。
    4. 公式：
      1. 余弦相似度：\mathrm{cos\_sim}(z_i^o,z_j^v)=\frac{z_i^o·z_j^v}{||z_i^o||_2\times ||z_j^v||_2}，归一化到[0,1]（加1除以2）
      2. 观测-虚拟节点双向对齐：
        1. 第j个虚拟节点的参考观测节点索引：Ind_v[j]=\mathrm{argmax}_{i\in[1,N_o]}M_{s[i,j]}
        2. 第j个虚拟节点与参考观测节点的相似度：S_v[j]=\mathrm{max}_{i\in[1,N_o]}M_{s[i,j]}
        3. 第i个观测节点的参考虚拟节点索引：Ind_o[i]=\mathrm{argmax}_{j\in[1,N_v]}M_{s[i,j]}
        4. 第i个观测节点与参考虚拟节点的相似度：S_o[i]=\mathrm{max}_{i\in[i,N_v]}M_{s[i,j]}
      3. 特征加权融合
        1. 虚拟节点特征融合：Z_j^{v,fused}=FC(Z_j^v||(S_v[j]\odot Z_{Ind_v[j]}^o))
        2. 观测节点特征融合：Z_i^{o,fused}=FC(Z_i^o||(S_o[i]\odot Z_{Ind_v[i]}^v))
      4. 输出融合特征
        1. 将所有虚拟节点的融合特征与观测节点的融合特征折整合，得到完整的节点融合特征矩阵Z^{fused}\in \mathbb{R}^{(N_o+N_v)\times D}

    image-20250831114759597

  4. 节点感知循环调节：NCR

    1. 作用：为虚拟节点提供伪标签监督，优化模型对未观测节点的插值精度
    2. 步骤：
      1. 第一次推理（生成初始伪标签）：输入观测节点数据X_{T-t:T}，通过克里金模块得到所有节点（观测节点+虚拟节点）的估计值\hat{X}_{T-t:T}，将虚拟节点的估计值作为初始伪标签
      2. 角色互换（构建反向掩码）：使用反向掩码(1-M_{T-t:T})（M为原始掩码，1表示观测节点），将虚拟节点的伪标签作为观测值，观测节点的真实值掩盖，得到X_{T-t:T}^c
      3. 第二次推理（循环调节）：基于X_{T-t:T}^c再次运行克里金模型，得到\hat{X}_{T-t:T}^c，通过两次估计值的MAE损失（伪标签损失）约束虚拟节点训练
      4. 总损失函数：结合观测节点的真是标签损失与伪标签损失，公式如下：L=MAE(\hat{X}_{T-t:T},X_{T-t:T},I_{obs})+\lambda·MAE(\hat{X}_{T-t:T}^c,X_{T-t:T}^c,I_{all})

    image-20250831114739457

实验部分

KITS

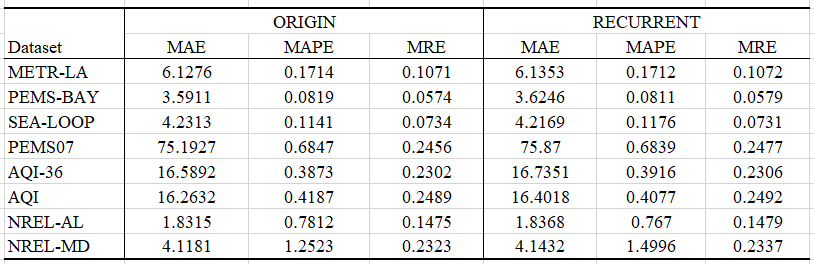
image-20250831114604057

Ablation

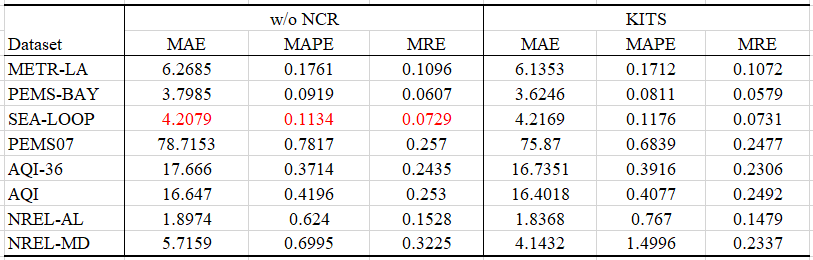
image-20250831114439521

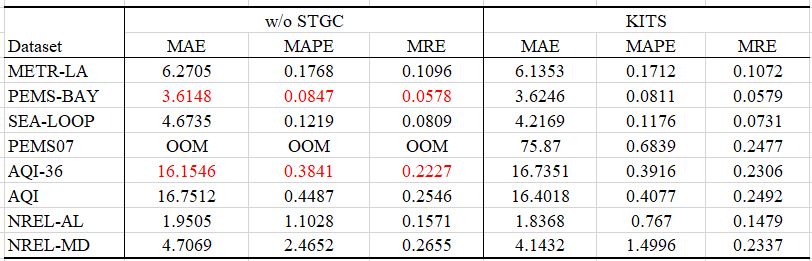
image-20250831114448333

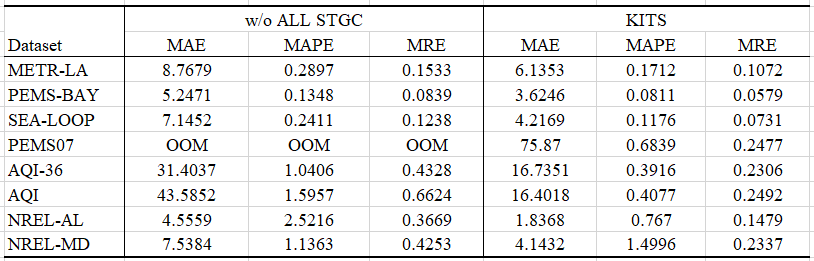
image-20250831114508146

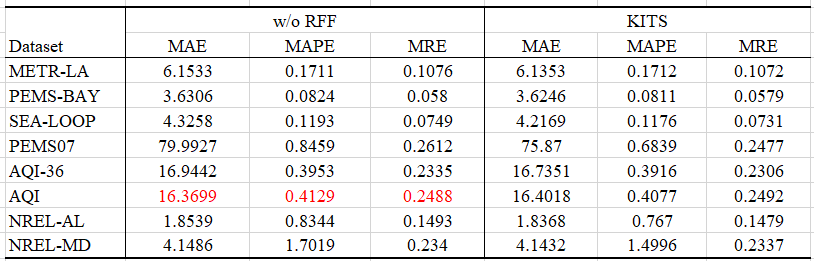
image-20250831114525834

Baseline

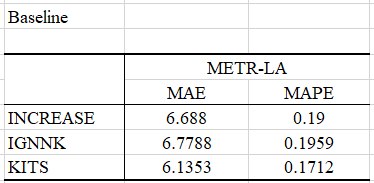
image-20250831114624213

hyperparameter