Report 20250804

论文：FC-STGNN

title: Fully-Connected Spatial-Temporal Graph for Multivariate Time-Series Data

arxiv: https://arxiv.org/abs/2309.05305

code: https://github.com/Frank-Wang-oss/FCSTGNN

创新点

1. 将所有时间戳的传感器进行全连接，通过传感器特征的点积计算相关性，直接建模 DEDT 依赖
2. 引入衰减矩阵（Decay Matrix），基于时间距离调整相关性权重，使图结构更符合实际时空规律
3. 设计移动池化 GNN 层（Moving-Pooling GNN），高效捕捉局部时空依赖
4. 实现对多元时间序列数据中 “全面时空依赖” 的建模

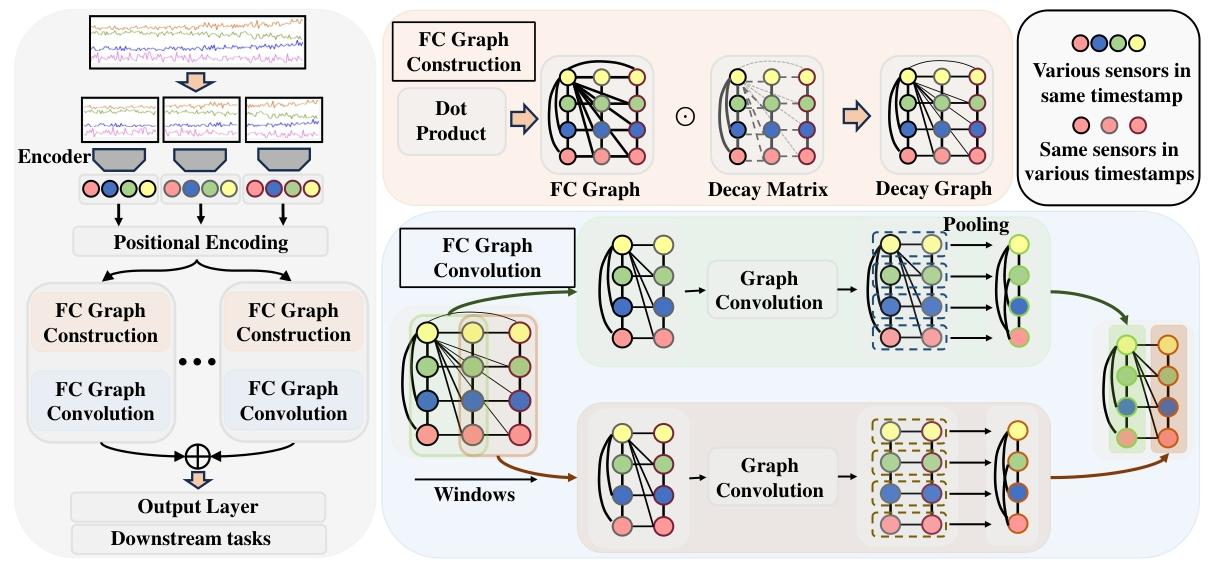
模块构成

1. 输入预处理模块
   1. 数据分块处理：将每个传感器捕获到的时序信号分割为多个连续局部片段（文中称为patch），每个patch对应一个时间戳
   2. 传感器级编码：使用1D-CNN作为传感器级编码，将每个patch中的信号进行编码，作用是学习传感器的局部（patch内的）时序特征
   3. 位置编码：引入类似Transformer的位置编码（正弦余弦位置编码），作用是保留patch之间的时间顺序信息
   4. 优点：
      1. 保留局部时序模式：分块操作聚焦于传感器信号的局部片段，避免长时序带来的噪声干扰
      2. 显式时间位置：位置编码确保模型能区分不同时间戳的 patch，为时间依赖建模奠定基础

2. FC 图构建模块

   1. 全连接图初始化：通过点积计算任意两个传感器的相关性$ e_{tr,ij}=g_s(z_{t,i})·(g_s(z_{r,j}))^T $，其中$g_s(z)=zW_s$（$W_s$可学习），$t,r$为patch索引，$i,j$为传感器索引，并通过$softmax$归一化到$[0,1]$，形成初始的邻接矩阵
   2. 衰减矩阵（Decay Matrix）：引入衰减矩阵$C$，$c_{tr,ij}=δ^{|t-r|}$ ，其中$δ∈(0,1]$为衰减率。最终的邻接矩阵为$e_{tr,ij}=e_{tr,ij}·c_{tr,ij}$，作用是引入时间距离的影响，使时间距离更近的传感器相关性更强

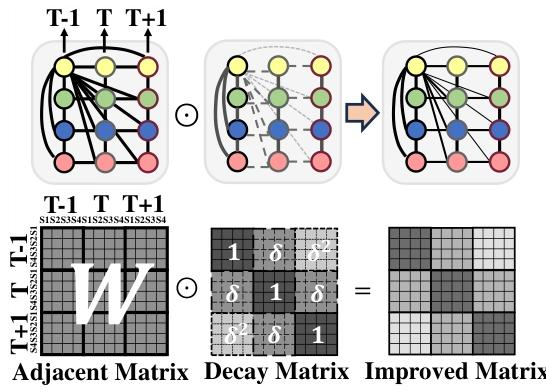
   3. 该模块构建了三种全连接图：

      1. 同patch内传感器的空间依赖($t=r$)
      2. 不同patch同一传感器的时间依赖($t \neq r ,i=j$)
      3. 不同patch不同传感器的DEDT依赖(Different sEnsors at Different Timestamps)($t \neq r ,i \neq j$)

   4. 优点：

      1. DEDT依赖解决了时空依赖建模不完整的问题
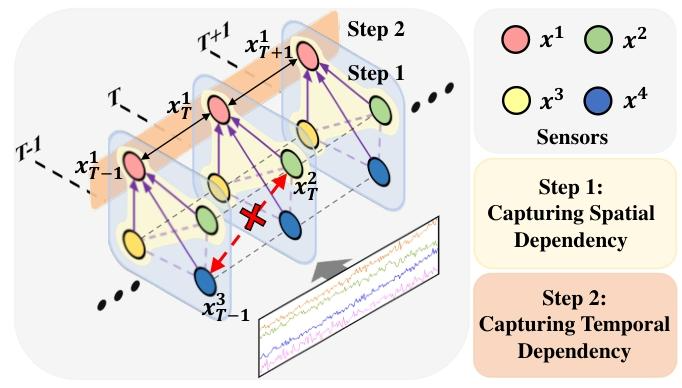
      2. 衰减矩阵使相关性更符合实际物理规律

3. FC图卷积模块

   1. 滑动窗口：使用大小为$M$的窗口在patch序列上滑动（步长为s）

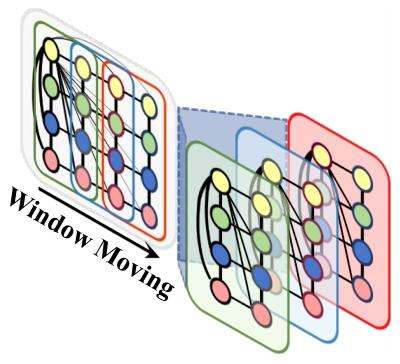
   2. 窗口内图卷积：对窗口内的子图才用消息传递神经网络（MPNN）进行卷积：

      1. 信息传播：中心节点$z_{t,i}^l$（第$l$层）聚合窗口内所有的邻居节点的特征，$h_{t,i}^l=\sum_{r\in窗口}\sum_{j=1}^Nz_{r,j}^l·e_{tr,ij}^l$，其中$e_{tr,ij}^l$为窗口内的归一化相关性权重
      2. 特征更新：通过非线性函数更新特征：$z_{t,i}^{l+1}=f_g(h_{t,i}^l|W_g)$，$W_g$为可学习，$f_g$为$\mathrm{ReLu}$
      3. 时间池化：对窗口内所有patch的传感器特征进行平均池化，得到窗口级高层特征$z_{w,i}^{l+1}=\frac{1}{M}\sum_{t\in窗口}z_{t,i}^{l+1}$，其中$w$为窗口索引
      4. 并行多层：多个并行的移动池化GNN层（使用不同的值初始化权重），从不同的视角捕捉时空依赖，最终拼接所有层的输出特征

   3. 优点：

      1. 使用滑动窗口，重点关注局部依赖，避免全局卷积造成大量运算
      2. 时间池化压缩窗口内的时序信息，减少特征维度和计算消耗
      3. 多并行层通过不同权重初始化捕捉多样化依赖，提升模型对复杂数据的适应能力
      4. MPNN 消息传递机制适配图结构，能有效利用全连接图中的相关性权重

4. 输出层

   1. 将前一个模块多个并行层拼接的特征通过MLP映射为最终结果：$h=\mathrm{MLP}(\mathrm{Concat}(z_w^1,z_w^2,...,z_w^K))$，$K$为并行层数

实验部分

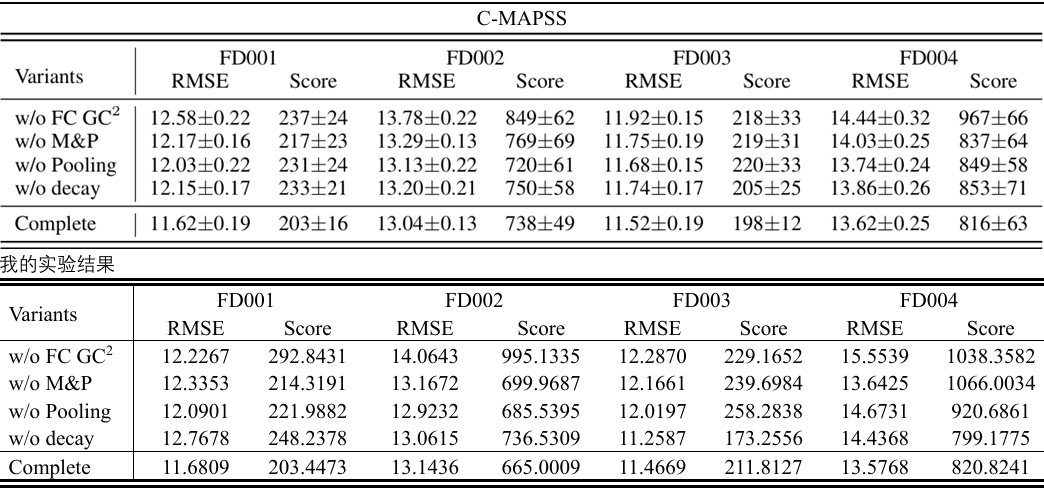
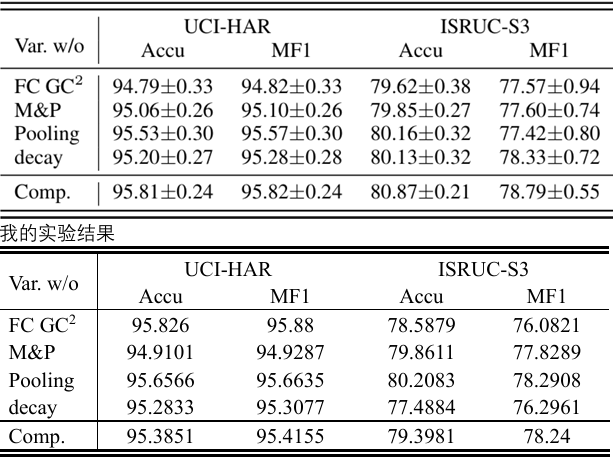
实验结果复现：

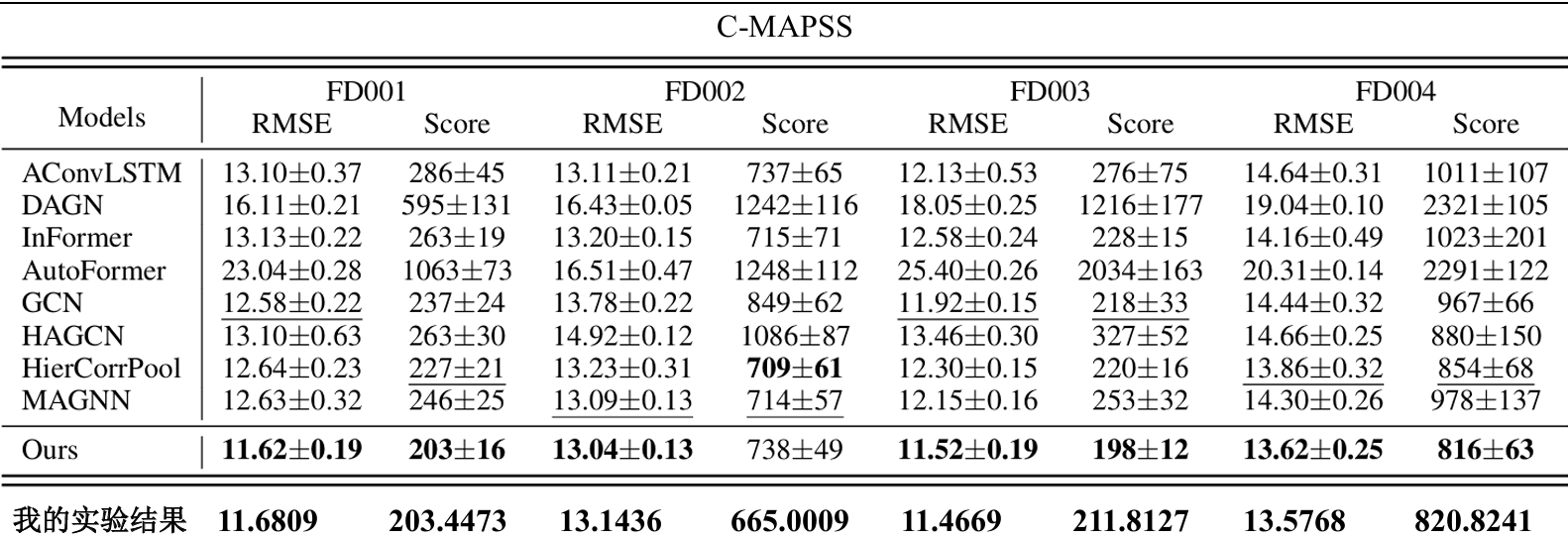
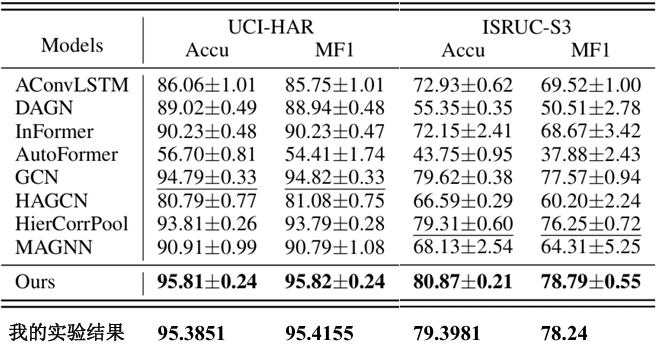
消融实验：