Report 20250721

论文1：ST-ReP

title: ST-ReP: Learning Predictive Representations Efficiently for Spatial-Temporal Forecasting

arxiv: https://arxiv.org/abs/2412.14537

创新点

提出了一套自监督学习框架，结合当前序列重建和未来值预测两部分，两者结合使模型学习到的表示既包含当前数据的语义信息，又具备对未来趋势的预测性，更适合下游时空预测任务
提出 C-E-D（压缩-提取-解压）的时空编码方案，用线性编码器捕捉变量间的相关性，大幅降低计算开销的同时，保证了对时空相关性的有效捕捉，提升了模型在大规模数据集上的可扩展性
损失函数结合了重建损失、预测损失和多尺度损失，从多个角度约束模型学习。
ST-ReP 在效率和可扩展性上具有优势，得益于轻量级设计，现有方法在大规模数据集上常遇到 OOM 问题，而 ST-ReP 能处理。

模块构成

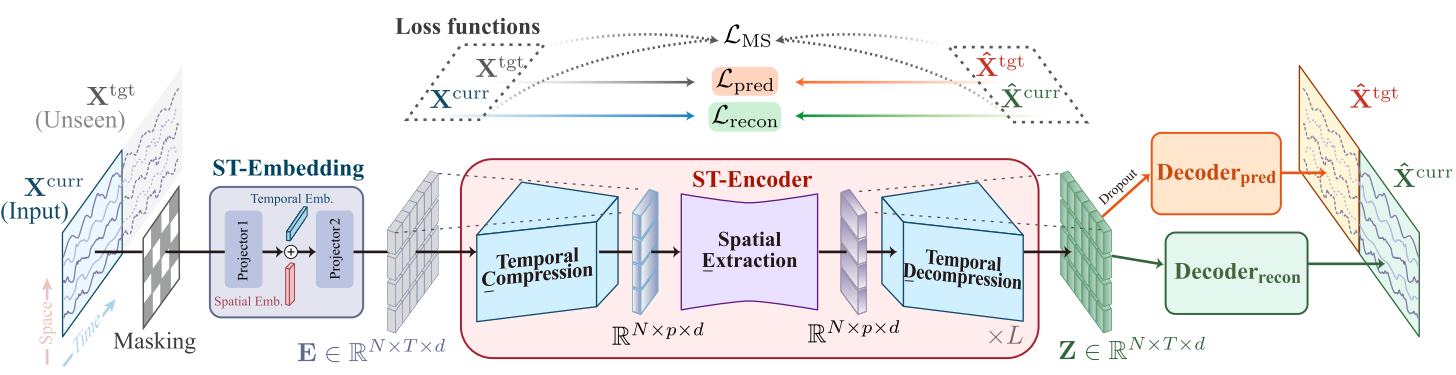
ST-Embedding 模块：将原始的数据集的时空数据转换为包含时空语义的嵌入向量。
1. 将mask tokens随机掩码后的数据经过两个线性层+ReLU激活，映射到隐藏空间，然后使用mask tokens来补齐序列长度，让输入的序列长度保持一致。
2. 将时空信息进行嵌入，时间嵌入+星期嵌入+空间嵌入，因为在此之前做了掩码，此处需要通过torch的广播机制来对各种嵌入进行相加
3. 对时间维度进行等宽卷积（这种卷积的输入输出尺寸相同），这种卷积可以使嵌入的信息更丰富
ST-Encoder模块：具有 C-E-D 结构的线性时空编码器：
1. 时间维度的压缩与解压
  1. 压缩：使用MLP层+GELU（新了解到的激活函数），将时间维度的特征进行压缩（高维->低维），这样可以减少时间维度的冗余，同时保留高层语义（有选择性的保留了能反应数据核心规律的高层信息）
  2. 解压：压缩后的特征经过空间特征提取（操作顺序：时间压缩->空间提取->时间解压）后，再通过MLP层恢复到原来的时间维度
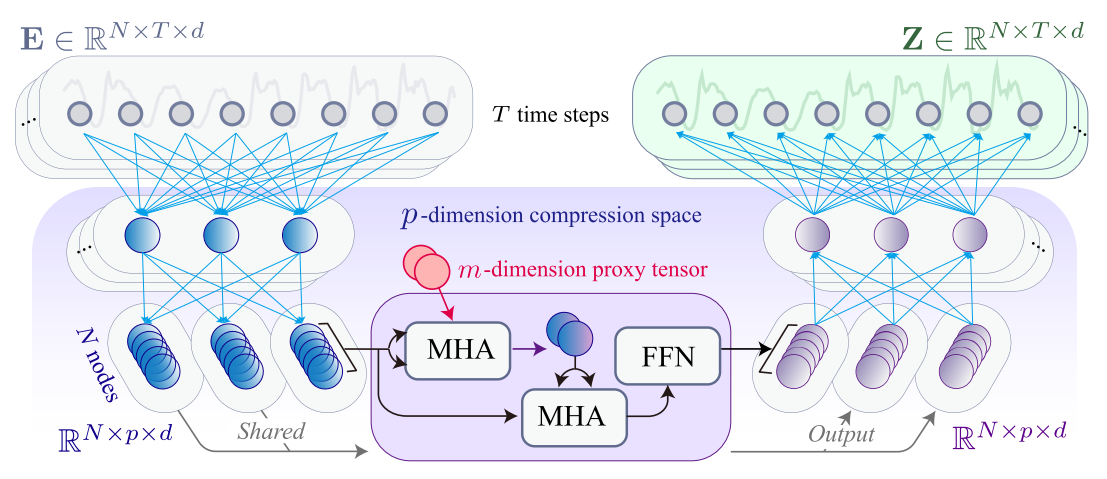
2. 空间维度的特征提取：基于代理张张量的线性空间编码器，用于捕捉空间相关性
  1. 代理张量（proxy tensor）：在计算注意力时作为查询（query），作用是在计算空间相关性的时候降低时间复杂度。
  2. 一共有两个多头注意力（MHA）层，第一个MHA以代理张量为查询，压缩后的特征为键值进行计算，得到一个中间结果，第二个MHA层以中间结果为键值，恢复特征到原始变量个数。
  3. 引入前馈网络（FFN）增强特征表达，整体计算复杂度与变量数量成正比，大幅降低冗余。
3. 因为输入输出维度都一样，多层ST-Encoder叠加（实验中用了3层叠加），然后与ST-Encoder层最初始的进行相加（残差连接）
解码器模块：重建与预测的双任务输出
1. 重建解码器：（线性层+残差连接+线性层+GELU）。重建解码器用于将多个ST-Encoder的最终数据输出映射到重建的当前值（指的就是没有被掩码的那一部分），用来计算重建损失
2. 预测解码器：（线性层+线性层+dropout），其中dropout是用来防止过拟合的。预测解码器用于将多个ST-Encoder的最终数据输出映射到未来值（指的就是被掩码的那部分，我们根据没被掩码的那部分想要预测出来的部分），用来计算预测损失
多尺度损失函数：约束模型学习多维度时空相关性
1. 包含了好几个损失（重建损失+预测损失+多尺度损失+总损失），消融实验中也对几个损失做了实验
2. 多尺度损失：将重建的当前值+预测的未来值结合形成一个完整的序列，与未经掩码的原始数据求损失，其中需要将两者经过多组不同大小的核进行平均池化（核分别为2,4,8,16）
3. 总损失：综合前几种损失计算加权平均（权重根据验证集上的最佳性能自动调整，{0.1,0.2,0.3,0.4,0.5}）

实验部分

实验结果复现：

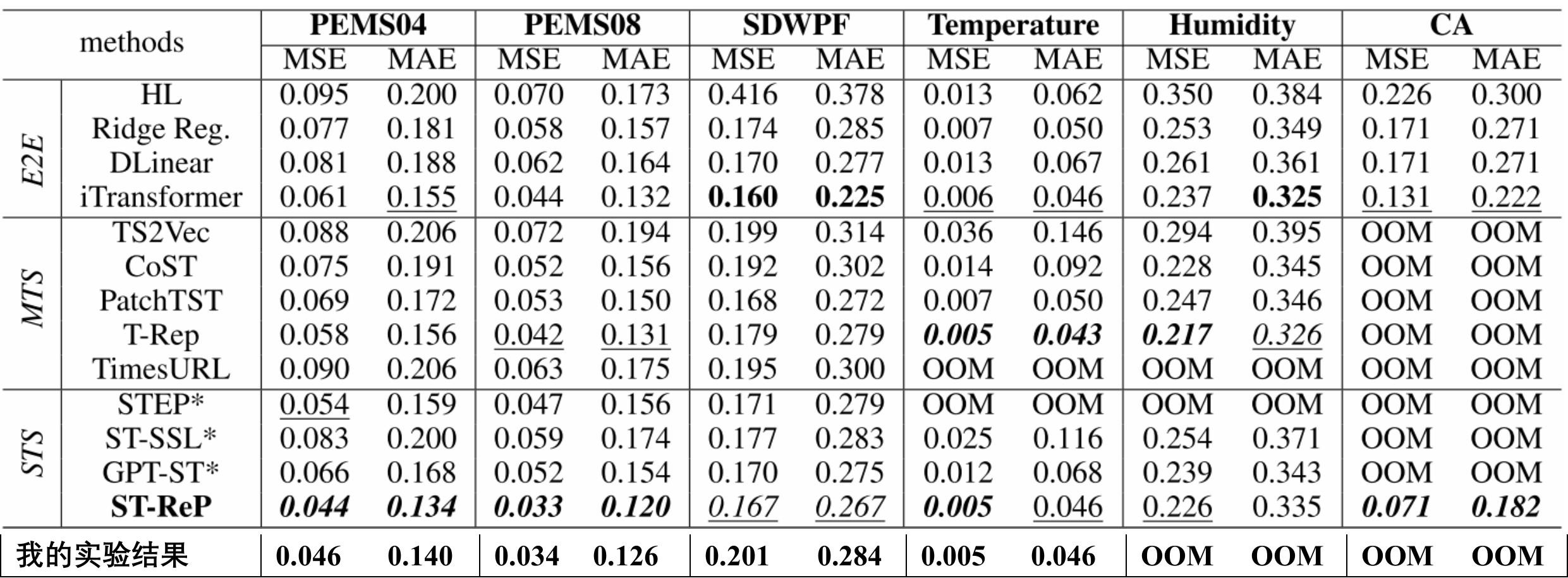
ST-ReP实验结果 - 常规

说明：Humidity和CA数据集在训练的时候会内存不足，直接被killed，我租的显卡服务器内存开到128G还是会爆内存。

消融实验：

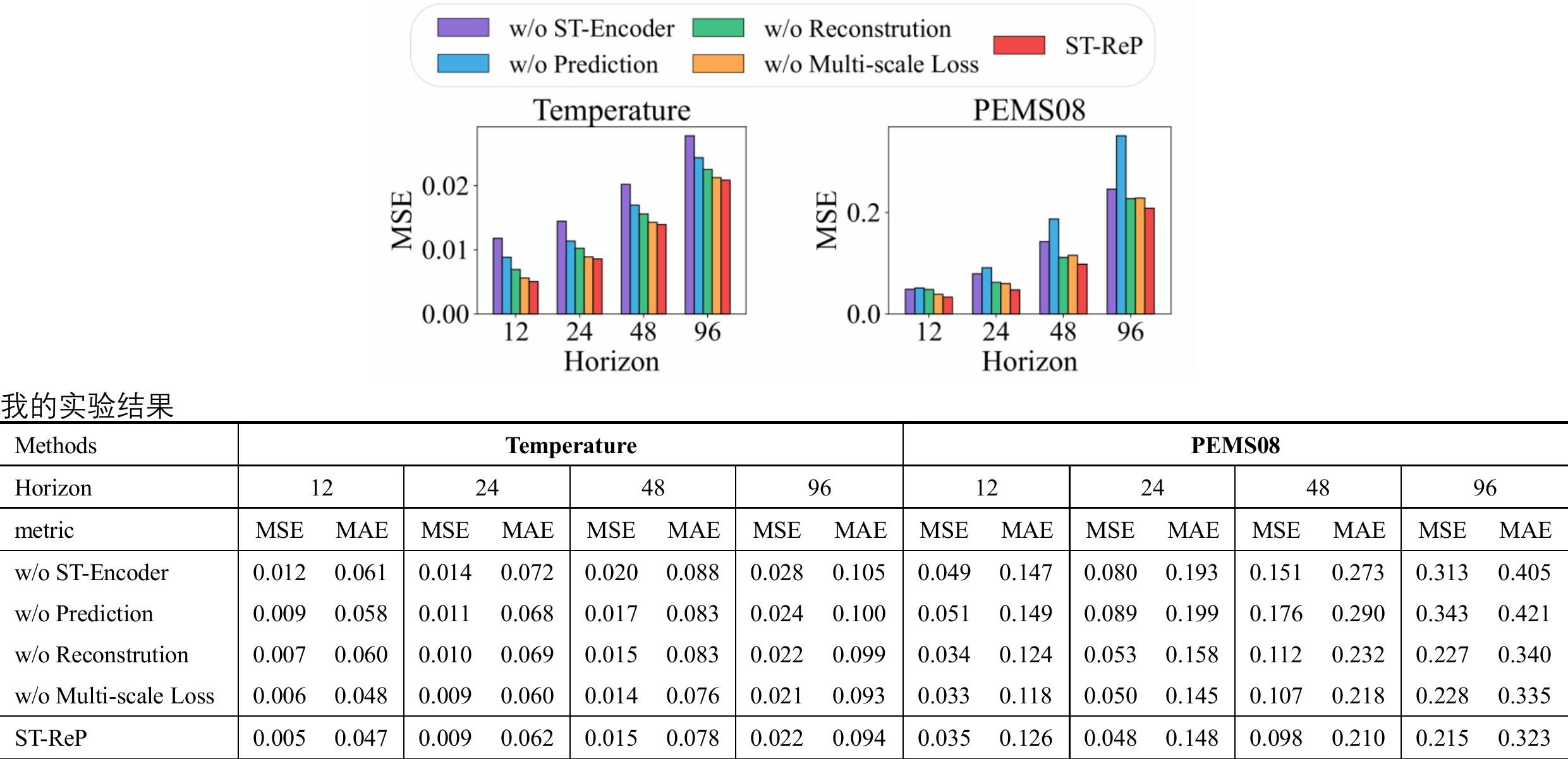
ST-ReP实验结果 - 消融

论文2：GeoAggregator

title: GeoAggregator: An Efficient Transformer Model for Geo-Spatial Tabular Data

arxiv: https://arxiv.org/abs/2502.15032

创新点

设计了轻量级 Transformer 架构，通过引入诱导点（inducing points）和优化的注意力机制，降低了计算复杂度，使其能高效处理大规模、高密度的地理空间数据集
多头部笛卡尔积注意力（MCPA）机制，在保持模型表达能力的同时，大幅减少可学习参数和计算量
高斯偏置注意力机制（Gaussian Attention Bias），使模型能更精准捕捉空间自相关，强化对邻近数据点的依赖建模
基于旋转矩阵的 2D 位置嵌入，相比传统位置嵌入，该方法更贴合地理空间的二维特性，提升了空间建模能力

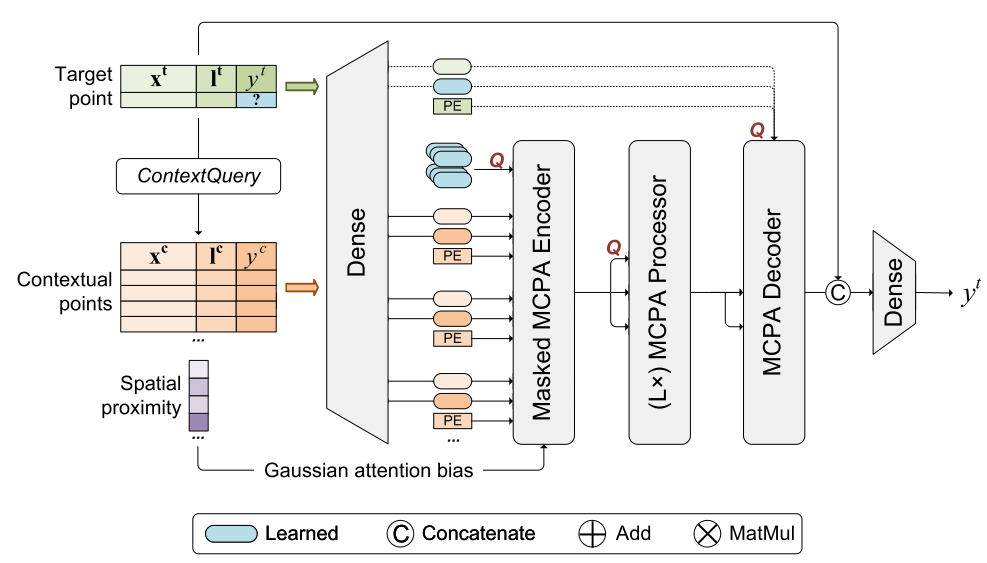
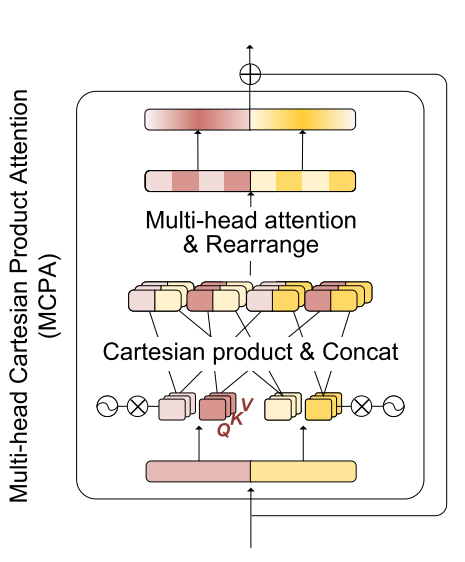
模块构成

输入序列处理：
1. 设定一个最大的接受长度（mini:81,small:144,large:256）
2. 对于每个目标点，通过ContextQuery映射来获取其空间临近的上下文点集合，如果这个点集合形成的序列长度大于最大接受长度则随机进行裁剪，如果小于最大接受长度则用0填充
3. 生成掩码序列，确保编码器只关注非0点
4. 这么做的目的是为了统一输入序列长度，过滤无效信息，其中的随机裁剪是防止模型依赖于上下文点的顺序
特征投影：
1. 构建两个并行的密集网络Dense_x和Dense_y，两个网络都使用Tanhshrink激活函数（Tanhshrink(x)=x−tanh(x)）
2. Dense_x将协变量 $x^{\{t,c\}}$ 投影到 $\mathbb{R}^{\frac{d_{model}}{2}}$ ，得到 $e_x$ 。（协变量指的是用于预测目标变量的辅助变量，包含各种特征）
3. Dense_y将上下文点的目标变量 $y^c$ 投影到 $\mathbb{R}^{\frac{d_{model}}{2}}$ ，得到 $e_y$ ；目标点的 $y^t$ 未知时，使用可学习的特征向量替代。（目标变量指的是需要预测的变量）
4. 目的是为了将原始协变量和目标变量转换为高维嵌入特征
2D 旋转位置嵌入
1. 先为每个点的空间位置生成正弦表示特征来构建4x4的2D旋转矩阵，再讲这些矩阵进行拼接，形成大的旋转矩阵，然后与嵌入特征进行矩阵乘法，实现位置信息的注入（ $e_x$ -> $\tilde{e}_x$ ， $e_y$ -> $\tilde{e}_y$ ）
2. 作用：解决Transformer的排列不变性问题，将2D空间的位置信息明确编码到特征中，确保模型能够铺捉到空间位置依赖关系（因为Transformer 模型对输入序列的元素的顺序不敏感，在处理需要跟位置信息有关联的任务时存在局限）
笛卡尔积注意力（MCPA）
1. 输入为特征投影后的协变量嵌入 $\tilde{e}_x$ 和目标变量嵌入 $\tilde{e}_y$ 。
2. 并行线性投影：通过线性层分别将 $\tilde{e}_x$ 和 $\tilde{e}_y$ 映射到 $\mathbb{R}^{d_c}$ 空间，得到两组嵌入 $\mathcal{X}$ 和 $\mathcal{Y}$ （每组含H个头）。
3. 笛卡尔积操作： $\mathcal{X}$ × $\mathcal{Y}$ = { $e_c = [x; y] | x \in \mathcal{X}, y \in \mathcal{Y}\}$ ，生成 $H^2$ 个头的注意力输出，最后通过线性投影重组为最终输出。
4. 在保持模型表达能力的同时，大幅减少可学习参数和计算复杂度
高斯偏置注意力：为了使注意力机制考虑空间相关性，向注意力机制中预先加入地理先验知识。使模型更关注临近点的信息。
编码器：
1. 包含一个 MCPA 操作，将上下文点的信息压缩到 “诱导点”（inducing points，即隐藏状态）中
2. 注入目标点的空间位置到诱导点，使每个诱导点能学习目标点与上下文点的位置交互模式
3. 作用是聚合上下文点的关键信息，通过诱导点减少后续计算的复杂度，建立目标点与上下文点的空间关联
处理器：
1. 含L个处理器模块（ $L=0,1,2$ 对应 GA-mini、GA-small、GA-large），通过诱导点间的交互学习全局空间模式。
2. 作用是降低全点注意力的计算复杂度，使计算复杂度随输入序列长度线性增长。
解码器与输出头：
1. 解码器为交叉注意力模块，用目标点查询诱导点的信息
2. 输出头为带 Tanhshrink 激活的密集网络，拼接解码后的嵌入与原始目标点特征（ $x_j^t$ 和位置 $l_j^t$ ），生成最终预测 $y_j^t$ 。
3. 作用是将诱导点的全局信息与目标点的局部特征相结合，输出预测结果

实验部分

实验结果复现：

GA实验结果 - 常规